2 Expérimentations pour comprendre la modélisation du frottement
Système étudié
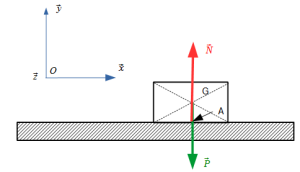
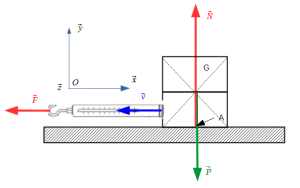
Pour expliquer le phénomène de frottement, nous allons étudier l'équilibre d'un bloc "S" sur un une table.
Bilan des actions mécaniques extérieures appliquées à S :
Action de la pesanteur sur S : \(\{T_{(terre\rightarrow S)}\} = \begin {array} {c}\\ \\\\\end{array} _G {\left \lbrace\begin{array} {cc}0 & 0\\-m.g & 0\\ 0 & 0\\\end{array} \right \rbrace}_{(\vec{x},\vec{y},\vec{z})}\)
Action de la table sur S : \(\{T_{(table\rightarrow S)}\} = \begin{array} {c} \\ \\\\\end{array} _A {\left \lbrace \begin{array} {cc}0 & 0\\N & 0\\ 0 & 0\\\end{array} \right \rbrace}_{(\vec{x},\vec{y},\vec{z})}\)
Remarque : on affecte la lettre N à la composante sur \(\vec y \)habituellement appelée Y. Il s'agit ici de bien faire remarquer que N est une composante normale (perpendiculaire) au contact.
Principe fondamental de la dynamique appliqué à S en A :
Théorème de la résultante :\(\Sigma \overrightarrow {F_{(ext\rightarrow S)}} = m \times \overrightarrow {A_{(G \in S /R)}}\)
Soit N - mg =0
Théorème du moment : inutile dans cette étude.
\(\Sigma \overrightarrow {M_{(A,ext\rightarrow S)}} =J _{(G, \overrightarrow{ z})}\times \frac {d \omega _{ (S/R)}}{dt} \overrightarrow z\)
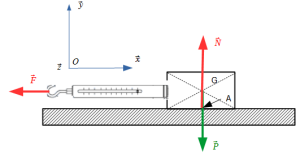
Simulation : Expérimentation n°1 : applique un effort F à S d'intensité modéré, le bloc S reste immobile.
Principe fondamental de la dynamique appliqué à S en A :
Théorème de la résultante \(\Sigma \overrightarrow {F_{(ext\rightarrow S)}} = m \times \overrightarrow {A_{(G \in S /R)}}\)
sur \(\vec x \) : -F = 0
sur \(\vec y \) : N - mg =0
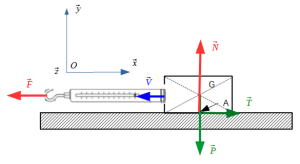
Or F est différent de 0 car mesuré sur le dynamomètre. Il manque dans la modélisation l'action due aux frottements T qui est donc sur l'axe \(\vec x \)et qui s'oppose au mouvement.
Conclusion :
La modélisation devient :
Action de la table sur S : \(\{T_{(table\rightarrow S)}\} : \begin{array} {c}\\ \\\\\end{array} _A {\left \lbrace \begin{array} {cc}T & 0\\N & 0\\ 0 & 0\\\end{array} \right \rbrace}_{(\vec{x},\vec{y},\vec{z})}\)
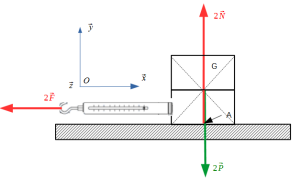
Simulation : Expérimentation n°2 : on augmente N en superposant 2 blocs. On peut augmenter F sans déplacer les blocs
Principe fondamental de la dynamique appliqué à S en A :
Théorème de la résultante :\(\Sigma \overrightarrow {F_{(ext\rightarrow S)}} = m \times \overrightarrow {A_{(G \in S /R)}}\)
sur \(\vec x \) : T-2F = 0
sur \(\vec y \) : 2 N - 2mg =0
Conclusion :
La composante T est proportionnelle à N. On peut écrire T =\(\mu\) N.
La modélisation devient :
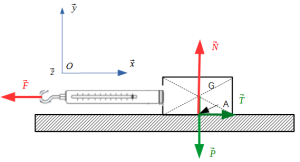
Action de la table sur S\(\{T_{(table\rightarrow S)}\} : \begin{array} {c}\\ \\\\\end{array} _A {\left \lbrace \begin{array} {cc}T=\mu N & 0\\N & 0\\ 0 & 0\\\end{array} \right \rbrace}_{(\vec{x},\vec{y},\vec{z})}\)
Simulation : Expérimentation n°3 : on augmente F jusqu'au début du déplacement des blocs
Principe fondamental de la dynamique appliqué à S en A :
Théorème de la résultante \(\Sigma \overrightarrow {F_{(ext\rightarrow S)}} = m \times \overrightarrow {A_{(G \in S /R)}}\)
sur \(\vec x \) : T-F = m.a x avec a x <0 (le bloc accélère "vers la gauche")
Donc T<F. L'action due aux frottements admet donc une limite.
Conclusion :
La modélisation devient T≤ k.N.
Action de la table sur S : \(\{T_{(table\rightarrow S)}\} : \begin{array} {c}\\ \\\\\end{array} _A {\left \lbrace \begin{array} {cc}T≤ kN & 0\\N & 0\\ 0 & 0\\\end{array} \right \rbrace}_{(\vec{x},\vec{y},\vec{z})} \).
