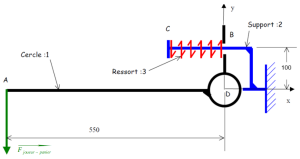
4 Exemple d'application
Mise en situation :
L'étude proposée repose sur un panier de basket muni d'un système à amortissement permettant, si le joueur reste pendu au panier, de pivoter librement évitant de ce fait de se plier de façon définitive.
Les 2 types de paniers :
Panier standard : Le cercle est en liaison encastrement avec le support donc sous l'effet d'une charge trop importante, le moment engendré peut faire plier l'ensemble : DANGER
Panier articulé : Le cercle est en liaison pivot avec le support, donc le mouvement avec le support est libre : SECURITE
Objectif : déterminer l'action du panier sur le ressort en fonction du poids du basketteur.
Constitution du système
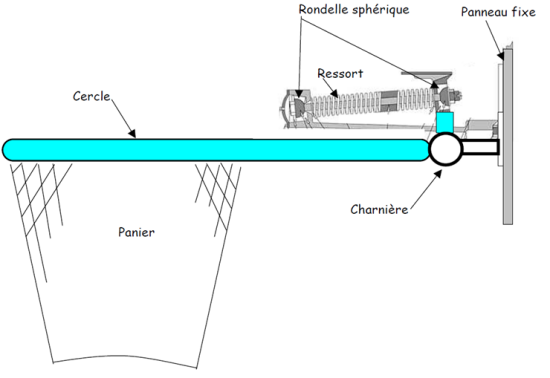
Modélisation
-les liaisons sont considérées sans jeu ni frottement.
-le poids des pièces est négligé
-on considère l'axe du ressort parallèle à l'axe x.
-les dimensions notées sur le schéma sont exprimées en mm.
Méthode : Partie1 : Isolement et Bilan des actions Mécaniques Extérieures :
On isole le cercle : 1.
Bilan des actions mécaniques extérieures à 1 et appliquées à 1 :
Action du ressort sur 1 :\({T_{(ressort\rightarrow1)}} : \begin{array} {c}\\ \\\\\end{array} _B {\left( \begin{array} {cc}X_{ressort \rightarrow 1}& 0\\0 & 0\\ 0 & 0\\\end{array} \right)}_{(\vec{x},\vec{y},\vec{z})}\)
Action du joueur sur 1 : \({T_{(joueur\rightarrow1)}} : \begin{array} {c}\\ \\\\\end{array} _A {\left( \begin{array} {cc}0 & 0\\-m.g & 0\\ 0 & 0\\\end{array} \right)}_{(\vec{x},\vec{y},\vec{z})}\)
Action du support 2 sur 1 (liaison pivot) :\({T_{(2\rightarrow1)}} : \begin{array} {c}\\ \\\\\end{array} _D {\left( \begin{array} {cc} X_{2 \rightarrow 1} &L_{1 \rightarrow 1} \\Y_{2 \rightarrow 1} & M_{2 \rightarrow 1} \\ Z_{2 \rightarrow 1} & 0\\\end{array} \right)}_{(\vec{x},\vec{y},\vec{z})}\)
Eciture du P.F.S et équations associées
Un système S est à l’équilibre si la somme des actions mécaniques extérieures est nulle :\(T(\bar{1} \rightarrow 1)= \vec{0}\).
Théorème de la résultante : \(\Sigma \overrightarrow {F(ext\rightarrow 1)} = \overrightarrow 0\):
e \(\overrightarrow {F_{ressort\rightarrow1}}+\overrightarrow {F_{joueur\rightarrow1}}+\overrightarrow {F_{2\rightarrow1}}=\vec0\)
Soit \(\left( \begin{array}{c}X_{ressort \rightarrow 1}+0+ X_{2 \rightarrow 1} =0 \\0 - m.g +Y_{2 \rightarrow 1}=0 \\ 0+0+Z_{2 \rightarrow 1}=0\\\end{array} \right)\)
Théorème du moment au point D :\(\Sigma \overrightarrow {M(D,ext\rightarrow 1)} = \overrightarrow 0\)
\(\overrightarrow {M _{(D,ressort \rightarrow 1)}} +\overrightarrow {M _{(D,joueur \rightarrow 1}}+ \overrightarrow {M _{(D,2 \rightarrow 1)}}= \vec0\)
Soit \(\left( \begin{array}{c}0+0+ L_{2 \rightarrow 1} =0 \\0 +0 +M_{2 \rightarrow 1}=0 \\ -0,1.X_{ressort \rightarrow 1}+0,55.m.g+0=0\\\end{array} \right)\)
Résolution
Pour répondre à l'objectif du problème (Rappel : déterminer l'action du panier sur le ressort en fonction du poids du basketteur), il faut chercher l'équation qui relie ces 2 termes : \( -0,1.X_{ressort \rightarrow 1}+0,55.m.g+0=0 \).
0n en déduit : \( X_{ressort \rightarrow 1}=\frac{0,55.m.g}{0,1} \).
Les autres équations peuvent utilisées mais pour répondre à d'autres objectifs :
Déterminer l'action du panier sur le bâti : \(\left| \begin{array}{c} X_{2 \rightarrow 1} =-X_{ressort \rightarrow 1} \\Y_{2 \rightarrow 1}= m.g \\ Z_{2 \rightarrow 1}=0 \\ L_{2 \rightarrow 1} =0\\M_{2 \rightarrow 1} =0\\\end{array} \right)\)