2.4 Modélisation des actions mécaniques associées aux liaisons
Fondamental : Propriété
La modélisation d'une liaison mécaniques permet de simplifier la modélisation de l'action mécanique transmissible par cette liaison.
Exemple : Modélisation de l'action mécanique transmissible par une liaison pivot glissant
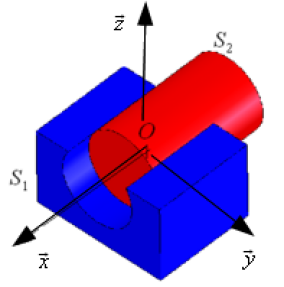
En supposant la liaison parfaite :
si l'on pousse S2 sur l'axe x, on ne pourra pas transmettre l'effort à S1: c'est S2 qui va se mettre en mouvement puisque la translation sur x est possible.
si l'on pousse S2 sur y, le mouvement n'est pas possible. On peut donc transmettre la force à S1.
si on exerce un moment sur S2 autour de l'axe x, on ne pourra pas transmettre le moment à S1: c'est S2 qui va se mettre en mouvement puisque la rotation sur x est possible.
si on exerce un moment sur S2 autour de l'axe y, le mouvement n'est pas possible. On peut donc transmettre le moment à S1
Remarque : on peut établir le même raisonnement pour l'action de S1 sur S2.
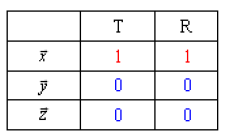
On vérifie alors la complémentarité des tableaux des degrés de liberté et de l'action mécanique modélisée.
\({T_{S2\rightarrow S1}} : \begin{array} {c}\\ \\\\\end{array} _O {\left( \begin{array} {cc}X_{S2 \rightarrow S1}=0 & L_{S2 \rightarrow S1}=0\\Y _{S2 \rightarrow S1}& M_{S2 \rightarrow S1}\\ Z_{S2 \rightarrow S1} & N_{S2 \rightarrow S1}\\\end{array} \right)}_{(\vec{x},\vec{y},\vec{z})}\)
soit \({T_{S2\rightarrow S1}} : \begin{array} {c}\\ \\\\\end{array} _O {\left( \begin{array} {cc}0 & 0\\Y _{S2 \rightarrow S1}& M_{S2 \rightarrow S1}\\ Z_{S2 \rightarrow S1} & N_{S2 \rightarrow S1}\\\end{array} \right)}_{(\vec{x},\vec{y},\vec{z})}\)