Mouvements de rotation et de translation
Fréquence de rotation et Vitesse Angulaire
On considère un système mécanique en rotation, par exemple l'arbre de sortie d'un moteur électrique ou d'un réducteur, le vilebrequin d'un moteur thermique,... dont la fréquence de rotation est notée N, en [tr/min].
On continue toutefois à employer aussi le terme de vitesse de rotation.
Remarque : Régime moteur
S'agissant d'un moteur thermique, on parle aussi de régime moteur.
Remarque : rpm
Les anglo-saxons utilisent comme unité [rpm] pour rev per minut (révolution par minute).
Ramenée en [tr/s] la fréquence de rotation N s'exprime grâce à la relation suivante :
\(N_{tr/s} = \frac {N_{tr/mn}} {60}\) |
Dans le Système International (S.I.), on exprime plutôt la fréquence de rotation par la vitesse angulaire \(\omega\), dont l'unité est le [rad/s].
Sachant qu'un tour correspond à \(2\pi\) radians, on peut écrire :
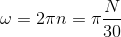
Vitesses angulaire et linéaire
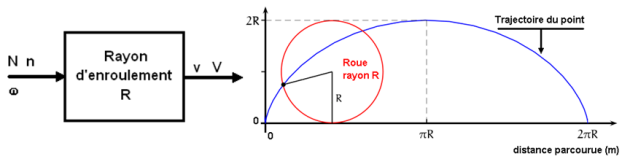
Le mouvement de rotation est souvent transformé en un mouvement de translation.
Exemple : Transformations rotation / translation
Déplacement de la cabine d'un ascenseur, obtenu grâce à un treuil (enroulement / déroulement d'un câble).
Déplacement d'un véhicule, la transformation s'effectuant grâce aux roues.
Le mouvement de translation est caractérisé par la vitesse linéaire v, exprimée en [m/s].
Elle dépend du rayon d'entraînement R, exprimé en [m]. Pour la roue R=D/2 où D est le diamètre.
Lorsque la roue fait un tour, la distance parcourue est égale au périmètre, soit \(2\pi R.\) Par conséquent, la vitesse linéaire v s'écrit :
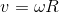
Remarque : Vitesse d'un véhicule
S'agissant d'un véhicule en mouvement et compte tenu des ordres de grandeur, il est plus aisé d'employer comme unité le [km/h]. Soit V la vitesse linéaire exprimée dans cette unité.
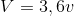
Remarque : mph
Les anglo-saxons utilisent le [mph] pour mile per hour (mile par heure). Un mile correspond approximativement à une distance de 1,6km.