Accélération, Vitesse, Déplacement
Un mouvement de translation (par exemple) s'effectue généralement en trois temps :
accélération
vitesse constante
décélération
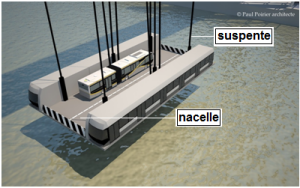
Exemple : Trajet d'une nacelle transbordée (d'après sujet Métropole juin 2015)
Pour assurer le confort des usagers de la nacelle et minimiser le phénomène de ballant, le mouvement obéit à un profil de vitesse trapézoïdal :
accélération (constante)
déplacement à vitesse constante
décélération (constante)
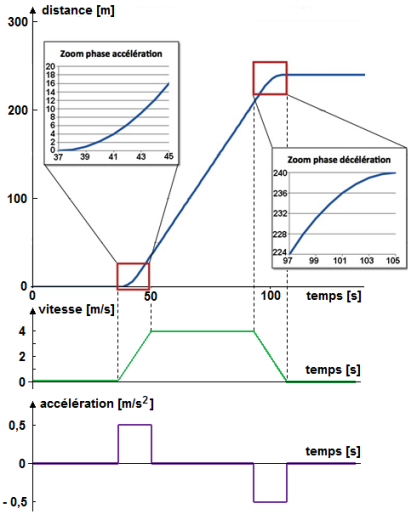
Les graphiques ci-dessous permettent d'observer que :
le déplacement se fait sans à-coup, il n'y a pas de brusque changement de pente s'agissant de la courbe distance = f(temps)
le déplacement à vitesse constante s'effectue à une vitesse \(v_{MAX}=4m \cdot s^{-1}\), ce qui correspond à 14,4km/h
la durée d'accélération (ou de décélération) est de 8s, pour une évolution de la vitesse (segment de droite) de 0 à 4m/s (ou de 4m/s à 0)
l'accélération \(acc\) est de ±0,5m/s2
Cette valeur est obtenue en faisant :
\(acc=\frac{v_{FINALE}-v_{INITIALE}}{t_{FINAL}-t_{INITIAL}}=\frac{4-0}{45-37}=0,5m\cdot s^{-2}\)
Remarque : Déplacement retour
Au retour, non représenté ci-dessus, la vitesse présenterait un profil similaire, avec toutefois des valeurs négatives, la vitesse est une grandeur algébrique.
Remarque : Vitesse moyenne
le déplacement proprement dit, hors phases de chargement/déchargement sur les quais, dure de t=37s à t=105s pour une distance totale parcourue de 240m, de quai à quai.
La vitesse moyenne du déplacement est donc :
\(v_{MOY}=\frac{d_{FINALE}-d_{INITIALE}}{t_{FINAL}-t_{INITIAL}}=\frac{240-0}{105-37}=3,53m\cdot s^{-1}\)
Cette vitesse moyenne est nécessairement inférieure à la vitesse \(v_{MAX}.\)
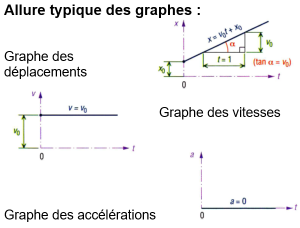
Fondamental : Mouvement Rectiligne Uniforme (MRU)
C'est le mouvement le plus simple, sans accélération (a=0) et donc avec une vitesse constante au cours du temps.
Équations de mouvement :
Équations de mouvement | avec |
|---|---|
x = v0t + x0 v = v0 = constante a = 0 | x : déplacement à l'instant t x0 : déplacement initial à t = 0 v0 : vitesse initiale du mouvement |
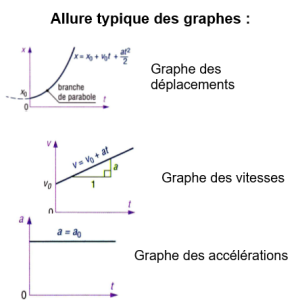
Fondamental : Mouvement rectiligne uniformément varié (MRUV)
Il sert de modèle à de nombreuses études simplifiées. Pour ces mouvements, accélérés (a>0) ou décélérés (a<0), l'accélération reste constante au cours du temps.
Équations de mouvement | avec |
|---|---|
Conditions initiales du mouvement : à t=0 : x=x0 ;v=v0 ;a=a0 x = 1/2 at2 + v0t + x0 v = at + v0 a = a0 = constante | x : déplacement à l'instant t x0 : déplacement initial à t = 0 v0 : vitesse initiale du mouvement a0 : accélération constante |
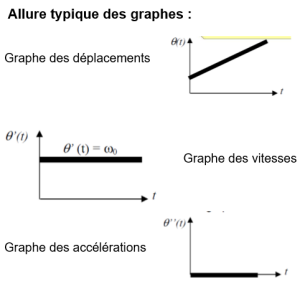
Fondamental : Mouvement circulaire uniforme (MCU)
Comme pour le mouvement rectiligne, un mouvement est uniforme si le vecteur vitesse angulaire est constant et le vecteur accélération angulaire est égal au vecteur nul.
Équations de mouvement | avec |
|---|---|
θ= ω0t + θ0 ω = ω0 = constante a = 0 | θ : déplacement à l'instant t θ0 : déplacement initial à t = 0 ω0 : vitesse initiale du mouvement |
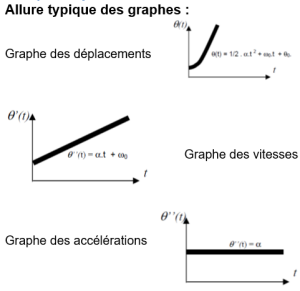
Fondamental : Mouvement Circulaire Uniformément varié (MRUV)
Comme pour le mouvement rectiligne, pour ces mouvements, accélérés (a>0) ou décélérés (a<0), l'accélération reste constante au cours du temps.
Équations de mouvement | avec |
|---|---|
Conditions initiales du mouvement : à t=0 : θ=θ0 ;ω=ω0 ;a=a0 θ = 1/2 at2 + ω0t +θ0 ω = at + ω0 a = a0 = constante | θ : déplacement à l'instant t θ0 : déplacement initial à t = 0 ω0 : vitesse initiale du mouvement a0 : accélération constante |
